Description of the Model
comet program is a Monte-Carlo/Lagrangian model that calculates the 3 dimensional positions of a large number of `nodes' representing material in an actin network. For each time step DELTA_T, nodes move a displacement proportional to the force acting upon them. There is no inertia, since this is a low Reynolds number regime. The forces acting on each node are as follows:
- Repulsive forces between nodes
- Link forces between nodes
- Link forces between node and nucleator
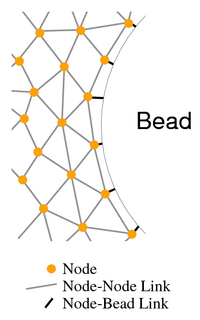
The nucleator object is treated as incompressible i.e. if during an iteration a node enters the nucleator, then in the next iteration it is simply moved out of the nucleator along a normal to the nucleator surface.
Nodes are nucleated at a constant rate, proportional to P_NUC , at the nucleator surface. To allow it to find an equilibrium position before being crosslinked into the network, a new node has its harbinger flag set when created, it experiences only repulsive forces for CROSSLINKDELAY iterations. Crosslinks are then formed as follows: All nodes with within XLINK_NODE_RANGE are counted, and links are either formed in random order, or if XLINK_NEAREST nearest first, until the number of crosslinks reaches MAX_LINKS_PER_NODE. Once a link is formed, its original distance is stored and used to calculate link forces. If the link is stretched or compressed away from its original length it behaves as a Hooke's Law spring and excerts a force proportional to, and opposing, the displacement. The scale multiple for this force is LINK_FORCE . This is to simulate an actin filament acting as an entropic spring by flexing motions. If the link force exceeds LINK_BREAKAGE_FORCE then the link breaks.
The nucleator is allowed to move and rotate, subject to displacement and torque vectors from the summed node repulsion from the nucleator, and the nucleator-node link forces. A full treatment of nucleator inertia is beyond the scope of the current model, and drag is simply scaled by a supplied parameter NUCLEATOR_INERTIA multiplied by the node inertia, and similarly the nucleator moment of inertia is scaled by the supplied parameter MofI . As a first approximation of how this should change with nucleator size, we scale the inertia and moment of inertia by the radius (or radius and length for long axes of the ellipsoids and capsules) if the VARY_INERT_W_RAD parameter is set. Given that this is not drag through a Newtonian fluid, but largely a product of complex fluid and network drag forces, this may not be very accurate. On the other hand the behavior is not very sensitive to the NUCLEATOR_INERTIA parameter anyway.
Output files are saved as jpgs for the x,y and z projections (convolved with a Gaussian to make it look like a microscope image). Post processing routines can produce 3D rendering jpgs, or interactive 3D renderings on-screen. Also, post-processing 3D rendering of a single image will trigger the program to also write a vrml file to allow the 3D view to be imported into other software (e.g. Acrobat 3D etc.). Note: the program calls the Imagemagick convert program to add text to the images and save as jpgs and calls bzip2 to compress the data files.